絶対に分かる機械学習理論

私が機械学習を学び始めたとき、訓練データとテストデータは異なるのだから、訓練データ上で損失を下げたとしても、テストデータでの性能が必ずしも保証されるとは限らないのではないかと感じ、理解に苦労しました。

本稿では、かつての自分を含め、統計と機械学習の初心者に向けて、なぜテストデータでも性能が理論的に保証されるのかを丁寧に解説します。

本稿の最後では、この議論を深層学習の理論に応用し、最先端の研究にまで一気に繋げます。期待値や分散などの統計学の基礎知識だけからここまで発展的な内容にまでたどり着くというのが本稿の目的です。ぜひ最後までお付き合いください。

目次

期待値への集中

まず、独立なデータの平均値が、期待値の周りに集中していく現象について議論します。

大数の法則は聞いたことがあると思います。サイコロを 1 個、10 個、100 個と転がした場合に、その平均値が期待値 に近づいていきます。

実際に、この現象を確認してみましょう。

まずはサイコロを一個振る場合。このときには当然、1 から 6 までが同じ割合で出ます。サンプルサイズは 1 なので、平均値 = 出た目の値です。

サイコロを一個振る場合の出目のヒストグラム。各値はほぼ同じ回数ずつ出ている。

続いて、サイコロを 10 個振り、その平均を求めるということを繰り返しましょう。一回の実験が 10 個のサイコロ振りに対応します。

10 個のサイコロを振る実験の結果。一行が一回の実験に対応する。

上の表のうち、赤で囲った最終列にある、平均値を可視化してみましょう。実験 1000 まで行い、1000 個の「平均値」をプロットしたのが以下の図です。

サイコロ 10 個の平均値のヒストグラム。値が 3.5 の周りに集まっている。

サイコロ 1 個の「平均値」とは様子が違います。値は 3.5 の周りに集まっていることが見てとれます。

続いて、100 個振ってみましょう。

100 個のサイコロを振る実験の結果。一行が一回の実験に対応する。

実験を 1000 回行い、1000 個の「平均値」をプロットしたのが以下の図です。

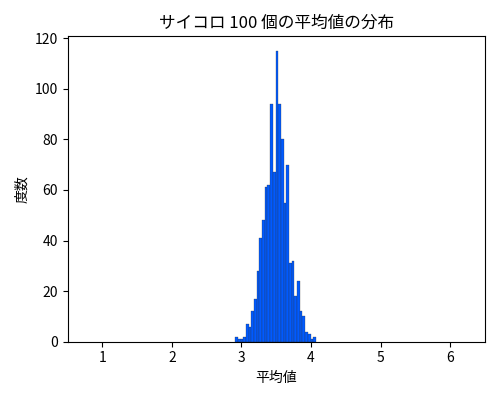サイコロ 100 個の平均値のヒストグラム。期待値の 3.5 にかなり集中している。

期待値の 3.5 にかなり集中していることが見て取れます。

最後に、10000 個振る場合が以下です。幅が見えないくらい 3.5 に集中しています。

サイコロ 10000 個の平均値のヒストグラム。幅が見えないくらい 3.5 に集中している。

このようにサンプルサイズ（= サイコロの個数）が増えるに従い標本平均は期待値 (=3.5) の周りに集中していきます。個数を無限に増やしていくと幅が見えないくらいになりほぼ確実に期待値にほぼ一致します。

以上では、この集中現象を実験的に確かめましたが、このことは統計の理論を使えば理論的にも保証できます。

マルコフの不等式

集中現象を表現した不等式のことを集中不等式 (concentration inequality) と言います。以下ではチェビシェフの不等式とヘフティングの不等式という2つの代表的な集中不等式を示します。まず、これ自体は集中不等式ではありませんが様々な集中不等式の基礎となるマルコフの不等式 (Markov's inequality) を紹介します。数学が苦手な方は不等式の意味と使い方だけ理解して証明については読み飛ばしても差し支えありません。

定理（マルコフの不等式）

非負の確率変数 と任意の定数 に対して、

\begin{align}\Pr(X \ge a) \le \frac{\mathbb{E}[X]}{a}\end{align}

が成立する。

マルコフの不等式は、期待値よりも極端に大きな値を取る確率が低いことを表しています。例えば、 とすると、

\begin{align}\Pr(X \ge 10 \mathbb{E}[X]) \le \frac{\mathbb{E}[X]}{10 \mathbb{E}[X]} = \frac{1}{10}\end{align}

となり、期待値よりも 10 倍以上大きな値を取る確率は 1/10 以下であることを表します。 これは考えてみれば当たり前で、期待値よりも 10 倍以上を取る確率が 1/10 より大きいなら、期待値を重み付き和で計算すると（期待値よりも 10 倍以上の値）×（1/10 より大きい値）の項が出てきて、その項だけで期待値を超えてしまうので矛盾します。このことを一般的な形で述べたのがマルコフの不等式です。

以下、補足の証明です。読み飛ばして問題ありません。

証明

非負の確率変数 と に対して、

\begin{align} \mathbb{E}[X] &= \int_{0}^{\infty} x\,p(x)\,dx \\ &= \int_{0}^{a} x\,p(x)\,dx + \int_{a}^{\infty} x\,p(x)\,dx \\ &\stackrel{(a)}{\ge} \int_{a}^{\infty} x\,p(x)\,dx \\ &\stackrel{(b)}{\ge} \int_{a}^{\infty} a\,p(x)\,dx \\ &= a\int_{a}^{\infty} p(x)\,dx \\ &= a\,\Pr(X \ge a) \end{align}

ここで、(a) は第一項が非負であることから、(b) は区間 において であることから従う。 で割ると、

\begin{align} \Pr(X \ge a) \le \frac{\mathbb{E}[X]}{a} \end{align}

が得られる。

チェビシェフの不等式

いよいよ、最初の集中不等式であるチェビシェフの不等式 (Chebychev's inequality) を示します。

定理（チェビシェフの不等式）

確率変数 が期待値 ] と分散 ] を持つとき、任意の に対して、

\begin{align}\Pr(|X-\mu| \ge k) \le \frac{\sigma^2}{k^2}\end{align}

が成立する。

チェビシェフの不等式は、期待値から値が極端に離れる確率が低いことを表しています。

例えば、 とすると、

\begin{align}\Pr(|X-\mu| \ge 10 \sigma) \le \frac{\sigma^2}{100 \sigma^2} = \frac{1}{100} \end{align}

となり、期待値から標準偏差 の 10 倍以上離れる確率は 1/100 以下であることを表します。

統計にある程度馴染みのある方は 2 シグマ範囲や 3 シグマ範囲という用語を聞いたことがあるかと思います。2 シグマ範囲は期待値からの乖離が標準偏差 の 2 倍までの範囲 、3 シグマ範囲は期待値からの乖離が標準偏差 の 3 倍までの範囲 のことです。チェビシェフの不等式によると、

\begin{align} \Pr(X \in [\mu - 2\sigma, \mu + 2\sigma]) &= \Pr(|X - \mu| \le 2 \sigma) \\ &\ge 1 - \Pr(|X - \mu| \ge 2 \sigma) \\ &\stackrel{\text{(a)}}{\ge} 1 - \frac{\sigma^2}{4 \sigma^2} \\ &= 1 - \frac{1}{4} \\ &= \frac{3}{4} \end{align}

同様に、

\begin{align} \Pr(X \in [\mu - 3\sigma, \mu + 3\sigma]) \ge 1 - \frac{1}{9} = \frac{8}{9} \end{align}

が得られます。(a) でチェビシェフの不等式を適用しました。つまり、確率変数は 以上の確率で 2 シグマ範囲に、 以上の確率で 3 シグマ範囲に収まります。2 シグマ範囲や 3 シグマ範囲は正規分布についてよく使われます。正規分布では約 95.45% の確率で 2 シグマ範囲に、約 99.73% の確率で 3 シグマ範囲に収まることが知られています。チェビシェフの不等式はこれよりも緩い保証ですが、正規分布に限らず、一様分布でも、二項分布でも、どんな分布でも成り立つ点が優れた点です。例えば機械学習モデルの損失分布は正規分布でも一様分布でもなく、名前も付けられないような複雑な分布ですが、そのような場合でもチェビシェフの不等式は適用でき、〇〇以上の確率で〇〇の範囲の値を取るということを導くことができます。この種の議論は本稿の後半で出てくるので、もう少しお待ちください。

チェビシェフの不等式は、 という確率変数にマルコフの不等式を適用することで証明できます。 は非負の確率変数で、期待値は です。これが より大きい値を取る確率をマルコフの不等式を用いて抑えることができます。

以下、補足の証明です。読み飛ばして問題ありません。

証明

確率変数 が期待値 ] と分散 ] を持つとき、非負の確率変数

\begin{align} Y = (X-\mu)^2 \end{align}

と置くと、その期待値は

\begin{align} \mathbb{E}[Y] = \mathbb{E}[(X-\mu)^2] = \sigma^2 \end{align}

となる。マルコフの不等式を に適用すると

\begin{align} \Pr(Y \ge k^2) \stackrel{\text{(マルコフの不等式)}}{\le} \frac{\mathbb{E}[Y]}{k^2} = \frac{\sigma^2}{k^2} \end{align}

が成り立つ。ここで、定義より

\begin{align} \{Y \ge k^2\} = \{(X-\mu)^2 \ge k^2\} \stackrel{\text{(平方根をとる)}}{=} \{|X-\mu| \ge k\} \end{align}

である。よって、

\begin{align} \Pr(|X-\mu| \ge k) = \Pr(Y \ge k^2) \le \frac{\sigma^2}{k^2} \end{align}

が従う。

チェビシェフの不等式の検証

実際にチェビシェフの不等式を検証してみましょう。

ここでは、先ほどのサイコロを振る実験を例にとり、チェビシェフの不等式がどのように適用できるかを確認します。まず、サイコロの出目の分散を求め、その後、標本平均の分散を導出し、最後にチェビシェフの不等式を適用します。

サイコロの出目の分散

サイコロの目 は 1 から 6 までの一様分布に従うため、期待値は です。分散は以下のように計算できます。

\begin{align} \mathrm{Var}(X) &= \mathbb{E}[(X - \mathbb{E}[X])^2] \\ &= \sum_{i=1}^{6} (i - 3.5)^2 \cdot \frac{1}{6} \\ &= \frac{(1 - 3.5)^2 + (2 - 3.5)^2 + (3 - 3.5)^2 + (4 - 3.5)^2 + (5 - 3.5)^2 + (6 - 3.5)^2}{6} \\ &= \frac{6.25 + 2.25 + 0.25 + 0.25 + 2.25 + 6.25}{6} \\ &= \frac{17.5}{6} \\ &= \frac{35}{12} \approx 2.92. \end{align}

標本平均の分散

サイコロを 個振り、その出目の平均をとると、標本平均 の分散は

\begin{align} \mathrm{Var}(\bar{X}) &= \mathrm{Var}\left( \frac{1}{n} \sum_{i=1}^{n} X_i\right) \\ &\stackrel{(a)}{=} \frac{1}{n^2} \mathrm{Var}\left( \sum_{i=1}^{n} X_i\right) \\ &\stackrel{(b)}{=} \frac{1}{n^2} (\mathrm{Var}( X_1 ) + \ldots + \mathrm{Var}( X_n )) \\ &\stackrel{(c)}{=} \frac{1}{n} \cdot \mathrm{Var}\left( X_1 \right) \\ &= \frac{35}{12 \times 10} \\ &= \frac{35}{120} \\ &= \frac{7}{24} \approx 0.292. \end{align}

となります。ここで、(a) は より、(b) は が独立であることから、(c) は が同分布であることから従います。つまり、サイコロ 個の標本平均 の分散は、各サイコロの出目の分散の 10 分の 1 です。

チェビシェフの不等式の適用

チェビシェフの不等式より、標本平均 が期待値 から 以上離れる確率は

\begin{align} \Pr(|\bar{X} - 3.5| \ge k) \le \frac{\mathrm{Var}(\bar{X})}{k^2}. \end{align}

です。

k = 1 の場合

\begin{align} \Pr(|\bar{X} - 3.5| \ge 1) &\le \mathrm{Var}(\bar{X}) = \frac{7}{24} \approx 0.292. \end{align}

この結果は、標本平均 が期待値から 1 以上ずれる確率が 0.292 以下であることを示しています。

実際、標本平均 が期待値から 1 以上ずれることはあまりありません。

の実験結果と のバウンド。チェビシェフの不等式は赤線の外に出る確率が 0.292 以下であることを保証し、実際、0.055 の割合でしか外に出ていない。

先に行った実験でも、期待値から 1 以上ずれた、つまり赤点線の外側に出た割合はわずか 0.055 でしかありません。たしかに、確率が 0.292 以下であるということは成り立っていそうです。

k = 1.5 の場合

\begin{align} \Pr(|\bar{X} - 3.5| \ge 1.5) &\le \frac{7}{24 \times (1.5)^2} \\ &= \frac{7}{24 \times 2.25} \\ &= \frac{7}{54} \\ &\approx 0.1296. \end{align}

標本平均 が期待値から 1.5 以上ずれる確率は 0.1296 以下であることが示されます。

の実験結果と のバウンド。チェビシェフの不等式は赤線の外に出る確率が 0.1296 以下であることを保証し、実際、0.004 の割合でしか外に出ていない。

実際、期待値から 1.5 以上ずれた、つまり赤点線の外側に出た割合はわずか 0.004 でしかありません。たしかに、確率が 0.1296 以下であるということは成り立っていそうです。

n = 100 の場合

サイコロを 個振ったときはどうでしょうか。標本平均の分散はサイコロの出目の分散の 100 分の 1、つまり であるので、標本平均 が期待値から 1 以上ずれる確率は 0.0292 以下、標本平均 が期待値から 1.5 以上ずれる確率は 0.01296 以下であることが示されます。つまり、そのようなことは滅多に起こらず、ほぼ確実に標本平均 は期待値から 1 以下のずれで収まるということです。実際、先に行った実験では、期待値から 1 以上ずれるということは 1000 回実験しても 1 回も起きていません。つまり割合にすると 0.001 以下です。

の実験結果と のバウンド。チェビシェフの不等式は赤線の外に出る確率が 0.0292 以下であることを保証し、実際、1 つも外に出ていない。

のときにはずれが 以上の確率が 以下とバウンドできました。 のときには、

\begin{align} \Pr\left(|\bar{X} - 3.5| \ge \frac{1}{\sqrt{10}}\right) &\le \frac{7}{240 \times \left(\frac{1}{\sqrt{10}}\right)^2} \\ &= \frac{7}{24} \end{align}

というように、 とより狭い範囲に入ることが同じ確率で保証できます。

の実験結果と のバウンド。チェビシェフの不等式より、70% 以上の確率で赤線の中に入ることが保証される。

このようにサンプルサイズを増やしていくと、幅を固定した場合には、その幅から外に出る確率がサンプルサイズに反比例して小さくなっていき、ほぼ確実にその幅の中に入るということが示せます。逆に確率の方を固定するとほぼ確実に入る幅というのがサンプルサイズの平方根に反比例して狭めていくことができます。これにより集中現象が理論的にも証明できました。

ヘフディングの不等式

チェビシェフの不等式は幅広い範囲で有用ではあるものの、裾の確率を緩く評価してしまうという弱点があります。サイコロを 100 個振った時に期待値から 1.5 以上離れるという現象ヒストグラムを見る限りまず起きそうにありません。

の実験結果と のバウンド。チェビシェフの不等式は赤線の外に出る確率が 0.01296 以下であることを保証し、実際、1 つも外に出ていない。

しかし、チェビシェフの不等式では 1% 程度はこれが起きるかもしれないとかなり呑気なことを言っています。このような裾の確率というのは期待値から遠ざかるにつれて指数的に減少することがよくあるのですが、チェビシェフの不等式では多項式 () のスピードでしか抑えられていません。これでは緩すぎて有用な理論結果が出ないことがよくあります。

そこで、このような裾の確率をより厳しく抑えるのに役立つのが次に紹介するヘフディングの不等式 (Hoeffding's inequality) です。

定理（ヘフディングの不等式）

を独立な確率変数、 をその標本平均とし、各 は区間 ] に値をとるとすると、任意の に対して

\begin{align} \Pr(|\bar{X} - \mathbb{E}[\bar{X}]| \ge t) \le 2 \exp\left(-\frac{2n^2 t^2}{\sum_{i=1}^{n}(b_i - a_i)^2}\right) \end{align}

が成立する。

すべての確率変数 が区間 に値をとる場合、ヘフディングの不等式は

\begin{align} \Pr(|\bar{X} - \mathbb{E}[\bar{X}]| \ge t) \le 2\exp(-2nt^2) \end{align}

とより簡潔な形になります。

ヘフディングの不等式の重要なポイントは、期待値からのズレの確率がサンプルサイズ とズレの幅 に応じて指数関数的に減少するということです。このため、サンプルサイズ・ズレの幅が大きい場合、ヘフディングの不等式はチェビシェフの不等式よりも遥かに強力な保証を与えます。

実際に先ほどのサイコロの例で、 とすると、

\begin{align} \Pr(|\bar{X} - 3.5| \ge 1.5) &\le 2 \exp\left(-\frac{2n^2 t^2}{\sum_{i=1}^{n}(6 - 1)^2}\right) \\ &= 2\exp\left(-\frac{2n t^2}{25}\right) \\ &= 2\exp(-18) \\ &\approx 0.0000000304 \end{align}

となり、実際に観察した結果（ほぼゼロ）とよく合致しています。チェビシェフの不等式がこの確率を約1%以下程度にしか評価できなかったことと比べると、ヘフディングの不等式の強力さがよく分かります。

以下、証明を掲載します。気になる方以外は読み飛ばして問題ありません。

証明

まず、以下の補題を証明する。

補題（ヘフディングの補題）

確率変数 が を満たし、 であるとする。任意の実数 に対して

\begin{align} \mathbb{E}\!\Bigl[e^{sX}\Bigr] \le \exp\Bigl(\frac{s^2(b-a)^2}{8}\Bigr) \end{align}

が成り立つ。

証明

まず、 であることから、 が成り立つ。 は の凸関数であるため、任意の ] に対して

\begin{align} e^{s x} \le \frac{b-x}{b-a} e^{s a} + \frac{x-a}{b-a} e^{s b} \end{align}

が成り立つ。 したがって、

\begin{align} \mathbb{E}\left[e^{s X}\right] &\le \mathbb{E}\left[\frac{b-X}{b-a} e^{s a} + \frac{X-a}{b-a} e^{s b}\right] \\ &=\frac{b-\mathbb{E}[X]}{b-a} e^{s a} + \frac{\mathbb{E}[X]-a}{b-a} e^{s b} \\ &= \frac{b}{b-a} e^{s a} + \frac{-a}{b-a} e^{s b} \\ &= e^{L\left(s (b-a)\right)} \end{align}

となる。ただし、

\begin{align} L(h) \stackrel{\text{def}}{=} \frac{ha}{b-a} + \ln\left(1+\frac{a-e^{h}a}{b-a}\right) \end{align}

と定義した。 微分を計算すると、

\begin{align} L(0) = L'(0) = 0, \quad L''(h) = \frac{-ab e^h}{\left(b - ae^h\right)^2} \end{align}

となる。 また、 であることから、 に対して相加相乗平均の不等式を適用すると、任意の に対して

\begin{align} \frac{-ab e^h}{\left(b - ae^h\right)^2} \le \frac{-ab e^h}{\left(2\sqrt{b\cdot(-ae^h)}\right)^2} = \frac{1}{4} \end{align}

が成り立つ。 さらに、テイラーの定理より、ある が存在して

\begin{align} L(h) = L(0) + hL'(0) + \frac{1}{2}h^2L''(h\theta) \le \frac{1}{8}h^2 \end{align}

となり、最終的に

\begin{align} \mathbb{E}\left[e^{s X}\right] \le e^{\frac{1}{8}s^2(b-a)^2} \end{align}

が得られる。 よって補題が示された。

---

以下、ヘフディングの不等式の証明に移る。 とする。 任意の に対して以下が成り立つ。

\begin{align} \Pr(\bar{X}-\bar{\mu}\ge t) &\stackrel{(a)}{\le} \Pr\Bigl(e^{sn(\bar{X}-\bar{\mu})}\ge e^{snt}\Bigr) \\ &\stackrel{(b)}{\le}\frac{\mathbb{E}\!\Bigl[e^{sn(\bar{X}-\bar{\mu})}\Bigr]}{e^{snt}} \\ &=\frac{\mathbb{E}\!\Bigl[e^{s\sum_{i=1}^{n}(X_i-\mu_i)}\Bigr]}{e^{snt}} \\ &=\frac{\mathbb{E}\!\Bigl[\prod_{i=1}^{n} e^{s(X_i-\mu_i)}\Bigr]}{e^{snt}} \\ &\stackrel{(c)}{=}\frac{\prod_{i=1}^{n}\mathbb{E}\!\Bigl[e^{s(X_i-\mu_i)}\Bigr]}{e^{snt}} \\ &\stackrel{(d)}{\le} \frac{\prod_{i=1}^{n}\exp\left(\frac{s^2(b_i-a_i)^2}{8}\right)}{e^{snt}} \\ &= \exp\Bigl(-snt+\frac{s^2}{8}\sum_{i=1}^{n}(b_i-a_i)^2\Bigr). \end{align}

が成り立つ。ここで、(a) は指数関数は単調なので であることから、(b) はマルコフの不等式から、(c) は独立性から、(d) は補題から従う。 ここで、 とおくと、

\begin{align} \Pr(\bar{X}-\bar{\mu}\ge t) &\le \exp\Biggl(-n t \cdot \frac{4nt}{\sum_{i=1}^{n}(b_i-a_i)^2} + \frac{1}{8}\left(\frac{4nt}{\sum_{i=1}^{n}(b_i-a_i)^2}\right)^2 \sum_{i=1}^{n}(b_i-a_i)^2\Biggr) \nonumber\\[1mm] &= \exp\Biggl(-\frac{4n^2t^2}{\sum_{i=1}^{n}(b_i-a_i)^2} + \frac{16n^2t^2}{8\sum_{i=1}^{n}(b_i-a_i)^2}\Biggr) \nonumber\\[1mm] &= \exp\Biggl(-\frac{4n^2t^2}{\sum_{i=1}^{n}(b_i-a_i)^2} + \frac{2n^2t^2}{\sum_{i=1}^{n}(b_i-a_i)^2}\Biggr) \nonumber\\[1mm] &= \exp\Biggl(-\frac{2n^2t^2}{\sum_{i=1}^{n}(b_i-a_i)^2}\Biggr). \end{align}

が得られる。同様の議論により、逆側の確率も

\begin{align} \Pr(\bar{\mu}-\bar{X}\ge t) \le \exp\Biggl(-\frac{2n^2t^2}{\sum_{i=1}^{n}(b_i-a_i)^2}\Biggr) \end{align}

が得られ、両側合わせて

\begin{align} \Pr\Bigl(|\bar{X}-\bar{\mu}|\ge t\Bigr) &= \Pr(\bar{X}-\bar{\mu}\ge t)+\Pr(\bar{\mu}-\bar{X}\ge t) \nonumber\\[1mm] &\le 2\exp\Biggl(-\frac{2n^2t^2}{\sum_{i=1}^{n}(b_i-a_i)^2}\Biggr). \end{align}

が示された。

モデルの評価

いよいよ機械学習理論に踏み込んでいきます。モデルの訓練については後で議論することにして、まずはモデルの評価について考えます。損失関数 はデータ に対するパラメータ の損失を表します。データ は入力と教師出力が組となった教師ありデータでもよいですし、入力のみの教師なしデータでもよいです。モデルの評価では、あらかじめ損失関数 およびパラメータ が与えられており、これらは評価を通して変化せず、固定されるものとします。

データ分布 から評価データ をサンプリングし、以下のように経験損失を計算します。

\begin{align} \hat{R}_n = \frac{1}{n} \sum_{i=1}^{n} \ell\bigl(X_i; \theta\bigr) \end{align}

一方、真のリスク（母平均）は、サンプリングされたデータだけでなくあらゆるデータを考慮して、次のように定義されます。

\begin{align} R = \mathbb{E}_{X\sim D}\Bigl[\ell\bigl(X; \theta\bigr)\Bigr] \end{align}

この母リスクは、モデルの真の良し悪しを表す未知の定数です。この値を明らかにして、モデルの真の性能を明らかにすることが評価の目的です。

各評価データ に対する損失値を表す確率変数を

\begin{align} Z_1 &= \ell\bigl(X_1; \theta\bigr) \\ Z_2 &= \ell\bigl(X_2; \theta\bigr) \\ \vdots & \\ Z_n &= \ell\bigl(X_n; \theta\bigr) \end{align}

と定義すると、経験損失は

\begin{align} \hat{R}_n = \frac{1}{n} \sum_{i=1}^{n} Z_i \end{align}

真のリスクは

\begin{align} R = \mathbb{E}[Z] \end{align}

と表されます。サイコロの実験でいうところ、各 はサイコロ の出目、真のリスク は期待値 に対応します。

サイコロの実験と同様に、評価データを 100 件サンプリングしてその経験損失 を計算する実験をくりかえしてみましょう。

評価データを 100 件サンプリングして経験損失 を計算する実験

この実験を 1000 回行い、1000 個の「平均値」をプロットしたのが下図です。

「評価データ 100 件の平均損失」の分布。0.37 付近に集中している。

期待値が と陽に求まったサイコロの例とは異なり、母平均 の具体的な値は事前には分かりません。しかし、図から が約 付近であると推察できます。

チェビシェフの不等式やヘフディングの不等式も、サイコロの実験と同様に適用できます。たとえば、チェビシェフの不等式を用いると、以下のように評価できます。

\begin{align} \Pr\Bigl(|R - \hat{R}_n| \ge k\Bigr) \le \frac{\mathrm{Var}(\hat{R}_n)}{k^2} = \frac{\mathrm{Var}(Z)}{nk^2} \end{align}

評価データ数 を十分に増やすことで、ほぼ確実に（例えば 99.99% の確率で）経験損失 が真のリスク から 以内に収まることが保証できます。つまり、有限個の、実際に使った評価データ だけから、まだ見ていないデータも含む、あらゆるデータについての真のリスク の情報が得られるということです。

訓練の場合には同じ議論は成り立たない

続いて、モデルの訓練について考えます。

損失関数 はあらかじめ決まっているものとします。訓練プロセスではまず、訓練データ をデータ分布からサンプリングします。訓練損失を

\begin{align} \hat{R}_n(\theta) = \frac{1}{n} \sum_{i=1}^{n} \ell\bigl(X_i; \theta\bigr) \end{align}

とし、訓練損失が最小となるパラメータを

\begin{align} \theta^\ast = \textrm{argmin}_{\theta} ~\hat{R}_n(\theta) \end{align}

として求めます。

ここで、もし訓練損失 が低ければ、母リスク

\begin{align} R(\theta^\ast) = \mathbb{E}\Bigl[\ell\bigl(X; \theta^\ast\bigr)\Bigr] \end{align}

も低いと言えるでしょうか。残念ながらこれまでの議論ではそれは言えません。これまでと何が違うのでしょうか。根本的な違いは をデータを見てから決めたということです は標本に依存するので も確率変数です。確率変数であることを強調するために大文字の で表記します。

前節の評価の場合、パラメータ はあらかじめ固定された定数であったため、各損失値

\begin{align} Z_1 &= \ell\bigl(X_1;\theta\bigr) \\ Z_2 &= \ell\bigl(X_2;\theta\bigr) \\ \vdots & \\ Z_n &= \ell\bigl(X_n;\theta\bigr) \end{align}

は互いに独立でしたが、今回の場合、前節と同様に を

\begin{align} Z_1 &= \ell\bigl(X_1;\Theta^\ast\bigr) \\ Z_2 &= \ell\bigl(X_2;\Theta^\ast\bigr) \\ \vdots & \\ Z_n &= \ell\bigl(X_n;\Theta^\ast\bigr) \end{align}

と定義しても、これらは確率変数 を共有しており、独立ではありません。これまでの議論は全て独立であることに依存していたので、もはや独立でなければ同じ議論は成り立ちません。

別の見方をすると、これは標本を見た後に仮説を決定したということです。たとえば、サイコロを振る前に出目を予測すれば、超能力でも使えない限り当たる確率は です。これは確率の話です。しかし、サイコロの出目を見た後に「絶対3が出ると思ってた〜」と言えば、「当たる確率」は でしょう。このように、後から情報を利用して仮説を決定すると、もはや確率論に基づく保証は成立しなくなります。

このため、サンプリングしたデータを見た上で評価対象を決定する機械学習の訓練では、きめ細かな仮定と議論が必要となり、理論的保証を付けるのが評価の場合よりもはるかに困難となります。

ユニオンバウンド

独立でない場合に使える強力な道具として、ユニオンバウンド (union bound) があります。ユニオンバウンドはブールの不等式 (Boole's inequality) とも呼ばれます。

定理（ユニオンバウンド）

任意の事象 について、

\begin{align} \Pr\Bigl(E_1 \cup E_2 \cup \cdots \cup E_N\Bigr) \le \Pr(E_1) + \Pr(E_2) + \cdots + \Pr(E_N) \end{align}

が成り立つ。

例えば、めったに起きない事象 の確率がそれぞれ

\begin{align} \Pr(E_1) &\le \epsilon_1 \\ \Pr(E_2) &\le \epsilon_2 \\ \Pr(E_3) &\le \epsilon_3 \end{align}

と抑えられているとすると、これらの事象のいずれか 1 つ以上が起きる確率は

\begin{align} \Pr\Bigl(E_1 \cup E_2 \cup E_3\Bigr) \le \epsilon_1 + \epsilon_2 + \epsilon_3 \end{align}

と抑えられます。考えるまでもなく、当たり前と思える人も多いでしょう。一応、完全性のために証明を入れておきますが、気になる方以外は読み飛ばしても差し支えありません。

証明

帰納法により証明する。 の場合は明らかに

\begin{align} \Pr(A_1) = \Pr(A_1) \end{align}

が成立する。 に対して

\begin{align} \Pr\left(\bigcup_{i=1}^{k} A_i\right) \le \sum_{i=1}^{k} \Pr(A_i) \end{align}

が成立すると仮定し、 のとき、

\begin{align} \Pr\Bigl(\bigcup_{i=1}^{k+1} A_i\Bigr) &=\Pr\Bigl(\Bigl(\bigcup_{i=1}^{k} A_i\Bigr)\cup A_{k+1}\Bigr)\\ &=\Pr\Bigl(\bigcup_{i=1}^{k} A_i\Bigr)+\Pr(A_{k+1}) -\Pr\Bigl(\Bigl(\bigcup_{i=1}^{k} A_i\Bigr)\cap A_{k+1}\Bigr)\\ &\stackrel{(a)}{\le} \Pr\Bigl(\bigcup_{i=1}^{k} A_i\Bigr)+\Pr(A_{k+1})\\ &\stackrel{(b)}{\le} \sum_{i=1}^{k}\Pr(A_i)+\Pr(A_{k+1})\\ &=\sum_{i=1}^{k+1}\Pr(A_i) \end{align}

となる。ここで、(a) は確率値が非負であることから、(b) は帰納法の仮定から従う。よって示された。

候補の数が有限の場合

パラメータの候補が の3つしかない場合を考えます。以下のような訓練プロセスを考えます。

(1) 訓練データ をデータ分布からサンプリングする

(2) 訓練損失を

\begin{align} \hat{R}_n(\theta) = \frac{1}{n}\sum_{i=1}^{n} \ell\bigl(X_i;\theta\bigr) \end{align}

と定義する。

(3) 全候補パラメータ について、訓練損失 を計算し、最も低いものを

\begin{align} \Theta^\ast = \textrm{argmin}_{\theta\in\{\theta_1,\theta_2,\theta_3\}} \hat{R}_n(\theta) \end{align}

として選択する。

通常、訓練では確率的勾配降下法などにより訓練損失 を最小化しますが、今回の例のように全候補を計算して一番良いものを選ぶ方法も立派な「最適化」です。また、データを見た後にパラメータを選ぶという訓練プロセスの本質も成立しています。

ここで、 は標本に依存する値であるため確率変数ですが、候補 は標本とは無関係にサンプリング前から存在する定数であることが重要です。 という候補から選ぶということは標本を見る前に確定していました。

そこで、 それぞれに対してチェビシェフの不等式を適用します。前節と同様に

\begin{align} Z_\theta = \ell\bigl(X;\theta\bigr) \end{align}

と定義し、母リスクを

\begin{align} R(\theta) = \mathbb{E}\Bigl[Z_\theta\Bigr] \end{align}

とします。

すると、チェビシェフの不等式により、

\begin{align} &\Pr\Bigl(|\hat{R}_n(\theta_1)-R(\theta_1)| \ge k\Bigr) \le \frac{\mathrm{Var}(Z_{\theta_1})}{nk^2} \\ &\Pr\Bigl(|\hat{R}_n(\theta_2)-R(\theta_2)| \ge k\Bigr) \le \frac{\mathrm{Var}(Z_{\theta_2})}{nk^2} \\ &\Pr\Bigl(|\hat{R}_n(\theta_3)-R(\theta_3)| \ge k\Bigr) \le \frac{\mathrm{Var}(Z_{\theta_3})}{nk^2} \end{align}

となります。これにユニオンバウンドを適用すると、

\begin{align} &\Pr\Bigl(|\hat{R}_n(\theta_1)-R(\theta_1)| \ge k \text{ or } |\hat{R}_n(\theta_2)-R(\theta_2)| \ge k \text{ or } |\hat{R}_n(\theta_3)-R(\theta_3)| \ge k\Bigr) \\ &\le \frac{\mathrm{Var}(Z_{\theta_1}) + \mathrm{Var}(Z_{\theta_2}) + \mathrm{Var}(Z_{\theta_3})}{nk^2} \end{align}

が得られます。つまりどれか一つでも乖離することはあまりない。これの余事象をとると

\begin{align} &\Pr\Bigl(|\hat{R}_n(\theta_1)-R(\theta_1)| < k \text{ and } |\hat{R}_n(\theta_2)-R(\theta_2)| < k \text{ and } |\hat{R}_n(\theta_3)-R(\theta_3)| < k\Bigr) \\ &\ge 1 - \frac{\mathrm{Var}(Z_{\theta_1}) + \mathrm{Var}(Z_{\theta_2}) + \mathrm{Var}(Z_{\theta_3})}{nk^2} \end{align}

というように、ほとんどの場合全てが乖離していないということを表します。サンプルサイズ を大きくすれば、ほぼ確実に の全ての訓練損失が母リスクに近いという状況が作り出せます。 は候補のいずれかなので、このとき

\begin{align} \Pr\Bigl(|\hat{R}_n(\Theta^\ast)-R(\Theta^\ast)| < k\Bigr) \ge 1 - \frac{\mathrm{Var}(Z_{\theta_1}) + \mathrm{Var}(Z_{\theta_2}) + \mathrm{Var}(Z_{\theta_3})}{nk^2} \end{align}

が保証されます。 は訓練後に訓練データで計算された損失です。これが、訓練データ以外も含むあらゆるデータを考慮した母リスク に近いということが、ほぼ確実に保証されます。

が小さいということは、 の選び方から（これが一番小さいものを として選んだので）分かっています。これに近い母リスク もやはり小さく、テスト性能も良いということです。

同様の議論は、パラメーターの候補 の数が有限である限り成立します。候補数が増えてきた場合には、ヘフディングの不等式による裾評価が生きてきます。

サイコロの例で見たように、例えば 、 の場合に対してヘフディングの不等式を使うと

\begin{align} \Pr(|\bar{X} - 3.5| \ge 1.5) &\le 2\exp(-18) \\ &\approx 0.0000000304 \end{align}

というように、確率が指数的に低い値となります。このとき、事象の候補が例えば 100 万個あっても、 なので、ユニオンバウンドを取っても大きなズレが起こる確率は 3% 程度に抑えられます。逆に言えば、候補数の増加に対して必要なサンプルサイズやズレの幅は、対数的な増加で十分ということです。これにより、かなりの数の候補があっても十分な保証が得られます。

候補の数が無限の場合

ヘフディングの不等式を使えば、かなりの数の候補を扱えるとはいえ、無限の候補があると扱いきれません。しかし、現実的にはパラメーターは や のように連続値を取り、候補は無限に存在します。無限の場合を扱うためには、さらに一工夫が必要です。それが カバリングナンバー (covering number) です。

定義（ε-被覆）

集合 の -被覆とは、集合 であって、これらを中心とする半径 の開球 を用いて を被覆できる、すなわち

\begin{align} A \subset \bigcup_{i=1}^{N} B(x_i,\epsilon) \end{align}

となるものを指す。

定義（カバリングナンバー）

集合 のカバリングナンバー とは、集合 の -被覆の要素数の最小値である。すなわち、

\begin{align} N(\epsilon,A) = \min\Bigl\{N \in \mathbb{N} \ \Bigl|\ A \subset \bigcup_{i=1}^{N} B(x_i,\epsilon)\Bigr\} \end{align}

と定義される。

-被覆の例。正方形内のどの点も距離 以内に代表点がある。

-被覆は代表点のようなものと考えてください。代表点は有限個なので、これらに対しては前節のようにユニオンバウンドを適用して理論保証ができます。また、代表点以外の点についても、 ほどの近さに代表点があり、その代表点については理論保証がされているので、そこから大きく離れていないということで理論保証ができます。

いくつか仮定を置いてバウンドを導出してみましょう。

まず、損失関数 を定義し、パラメータ をランダムに初期化します。訓練データ をサンプリングし、勾配降下法（でもなんでもよい）を用いて、訓練損失

\begin{align} \hat{R}_n(\theta) = \frac{1}{n}\sum_{i=1}^{n} \ell\bigl(X_i;\theta\bigr) \end{align}

を最小化することで、パラメータ を得ます。

ここで、以下のような仮定を置きます。

(1) 訓練により得られる最終的なパラメーター は、

\begin{align} \mathcal{H} = \Bigl\{\theta \in \mathbb{R}^d : \|\theta\| \le R\Bigr\} \end{align}

に含まれるとする。これは正則化や正規化などのテクニックで保証できます。

(2) 損失 は 0 以上 1 以下の値を取ると仮定する。これは損失のスケールを正規化することで保証できます。

(3) 損失 は、パラメーター に関して -リプシッツ 連続であり、

\begin{align} \|\theta_1 - \theta_2\| \le \epsilon \Rightarrow \bigl|\ell\bigl(X;\theta_1\bigr)-\ell\bigl(X;\theta_2\bigr)\bigr| \le L \epsilon \end{align}

とする。つまりパラメーターを少量動かしても（モデルの出力および）損失の値はほとんど変わらないということです。

パラメーター候補 ですが、これは d 次元立方体 に含まれています。

この立方体 を、一辺が の大きさの小立方体にさいの目状に区切ります。各小立方体の中心の集合を とおくと、 は の -被覆です。各中心点の球は自分の担当する小立方体をすっぽり覆っており、全点合わせるとすべての小立方体、ひいては を覆っているからです。各小立方体の数は、立方体の一辺の長さ に対して、一辺あたり約 個となるため、 および のカバリングナンバーは

\begin{align} N(\mathcal{H};\epsilon) \le \left\lceil \frac{\sqrt{d}R}{\epsilon} \right\rceil^d \end{align}

と抑えられます。特に、 とすると、

\begin{align} N\left(\mathcal{H};\frac{1}{4nL}\right) \le \left\lceil 4\sqrt{d}RnL \right\rceil^d \end{align}

です。

に最も近い 内の点を

\begin{align} \hat{\Theta}^\ast = \textrm{argmin}_{\theta \in \mathcal{C}} \|\Theta^\ast - \theta\| \end{align}

と定義すると、上記の被覆性から となります。

各代表点 に対して、前節と同様にヘフディングの不等式を用いれば、

\begin{align} \Pr\Bigl(|\hat{R}_n(\theta) - R(\theta)| \ge t\Bigr) &\le 2\exp\Bigl(-\frac{2n^2 t^2}{\sum_{i = 1}^n (1 - 0)^2}\Bigr) \\ &= 2\exp\Bigl(-2n t^2\Bigr) \\ \end{align}

となります。

ユニオンバウンドを用いると、

\begin{align} \Pr\Bigl(\exists\, \theta \in \mathcal{C}:\; |\hat{R}_n(\theta)-R(\theta)| \ge t\Bigr) \le 2 N(H;\epsilon) \exp\Bigl(-2n t^2\Bigr) \end{align}

となります。

ここで、

\begin{align} \epsilon &= \frac{1}{4nL} \\ t &= \sqrt{\frac{d \log \left(200 \left\lceil 4\sqrt{d}RnL \right\rceil\right)}{2n}} \end{align}

とおき、上記のユニオンバウンドに代入すると、

\begin{align} \Pr\left(\exists\, \theta \in \mathcal{C}:\; |\hat{R}_n(\theta)-R(\theta)| \ge \sqrt{\frac{d \log \left(200 \left\lceil 4\sqrt{d}RnL \right\rceil\right)}{2n}}\right) \le 0.01 \\ \Pr\left(\forall\, \theta \in \mathcal{C}:\; |\hat{R}_n(\theta)-R(\theta)| < \sqrt{\frac{d \log \left(200 \left\lceil 4\sqrt{d}RnL \right\rceil\right)}{2n}}\right) \ge 0.99 \\ \end{align}

というように、99% 以上の確率で、全ての代表点で訓練誤差と母リスクの差が 以下となります。特に、 なので、この点についてもこれが保証されます。以下、99% 以上の確率で成立するこの事象が成り立つものとします。

は -リプシッツ連続であり、 なので、

\begin{align} |\hat{R}_n(\Theta^\ast)-\hat{R}_n(\hat{\Theta}^\ast)| &= \left|\frac{1}{n} \sum_i \ell(X_i; \Theta^\ast)-\frac{1}{n} \sum_i \ell(X_i; \hat{\Theta}^\ast))\right| \\ &\le \frac{1}{n} \sum_i \left|\ell(X_i; \Theta^\ast)-\ell(X_i; \hat{\Theta}^\ast))\right| \\ &\le \frac{1}{n} \sum_i \varepsilon L \\ & =\varepsilon L \end{align}

および

\begin{align} |R(\Theta^\ast)-R(\hat{\Theta}^\ast)| &= \left|\mathbb{E}[\ell(X; \Theta^\ast)]-\mathbb{E}[\ell(X; \hat{\Theta}^\ast)]\right| \\ &\le \mathbb{E}\left[\left|\ell(X; \Theta^\ast)-\ell(X; \hat{\Theta}^\ast)\right|\right] \\ &\le \mathbb{E}[\varepsilon L] \\ & =\varepsilon L \end{align}

が成り立ちます。ゆえに、三角不等式より

\begin{align} |\hat{R}_n(\Theta^\ast)-R(\Theta^\ast)| &\le |\hat{R}_n(\Theta^\ast)-\hat{R}_n(\hat{\Theta}^\ast)| + |\hat{R}_n(\hat{\Theta}^\ast)-R(\hat{\Theta}^\ast)| + |R(\Theta^\ast)-R(\hat{\Theta}^\ast)| \\ &\le \varepsilon L + t + \varepsilon L \\ &= 2 \varepsilon L + t \\ &= \frac{1}{2n} + \sqrt{\frac{d \log \left(200 \left\lceil 4\sqrt{d}RnL \right\rceil\right)}{2n}} \\ &\le 2 \sqrt{\frac{d \log \left(200 \left\lceil 4\sqrt{d}RnL \right\rceil\right)}{2n}} \end{align}

となります（最後の不等式は分子が 1 以上のとき、あるいは漸近的に成り立ちます）。 は訓練後に訓練データで計算された損失です。これが、訓練データ以外も含むあらゆるデータを考慮した母リスク に近いということが、ほぼ確実に保証されます。

このバウンドからいくつか分かることがあります。まず、右辺が 1 以下となる有用なバウンドを得るためには、データ数 はパラメータの次元数 以上のオーダーである必要です。データ数がパラメータ数より少ないと、パラメータが不定になってしまいます。これは直感的にも納得できると思います。バウンドは の平方根におおよそ反比例して小さくなります。大雑把な議論ですが、対数成分は無視できるとするならば、パラメータの次元数の 100 倍のデータがあれば、訓練性能とテスト性能の差がだいたい 程度で抑えられるということです。

深層学習の理論へ

ここまでがいわゆる古典的な学習理論です。深層学習では、パラメータの数は数百万から数百億にものぼり、オーバーパラメタライズ、すなわちパラメータの次元数 が訓練データ数 よりも大きいことが一般的です。前節で見たように、古典的な学習理論では の場合、バウンドの値が 1 以上となり、意味のある保証をすることができません。このため、古典的な学習理論では、深層学習がなぜうまくいくのかを説明できないという問題が指摘されています。古典的な学習理論では深層学習がなぜうまくいくのかを説明ができないということは皆さんももしかしたら聞いたことがあるかもしれません。深層学習のようにオーバーパラメタライズしている場合でもテスト精度に対して有用な保証をするのは現在でも完全に解決したわけではありません。ここでは方針の1つを提示したいと思います。

深層ニューラルネットワークの損失地形のイメージ図

深層ニューラルネットワークの損失地形は、上図のように広大な盆地と先鋭な谷からなります。確率的勾配降下法を用いてモデルを訓練すると、先鋭な谷からは飛び出してほぼ確実に広大な盆地に収束することが知られています。よく訓練されたモデルは量子化したり精度を落としてもうまく動作します。これはぴったりそのパラメータ である必要はなく、ある程度ブレても損失は低い値であるということで、広い盆地にいることはこのことからもわかります。最終的なパラメータは、先鋭な谷には留まらず、必ず広大な盆地に収束すると仮定します。先鋭な谷に陥ってしまった場合は、盆地に収束するまでリスタートするように訓練すれば、このことは保証できます。

盆地の内側では縦横に動いても損失はほとんど変化しませんから、盆地からは代表点を1つ選べば十分です。そして、広大な盆地の数はそれほど多くありません。極端には、確率的勾配降下法で現実的にたどり着ける盆地は本質的には 1 つしかない（なのでパラメータの単純平均によるモデルマージがうまくいく）という説や、それほどではないにしても、盆地と推論方法は本質的に一対一に対応しており、うまくいかない推論方法は数あれどうまくいく推論方法のパターンは限られているため、学習後に辿り着きうる盆地は本質的には定数個しか存在しないという説もあります。

やや粗い議論ですが、もし盆地の個数が定数 個で、標本によらず毎回この 個のいずれかに収束すると仮定できるならば、前節の議論と同様に、確率

\begin{align} 1 - 2K \exp\Bigl(-2n t^2\Bigr) \end{align}

で誤差

\begin{align} t + (\text{盆地内での損失の変動}) \end{align}

を達成できます。ここで とすると、確率 99% で誤差が

\begin{align} \sqrt{\frac{\log(200K)}{2n}} + (\text{盆地内での損失の変動}) \end{align}

となる保証が得られます。このバウンドはパラメータの次元 に依存しません。

本当に本質的な盆地の個数が定数個しか存在しないのか、またどのような条件下でその性質が成り立つのかは、現在でもはっきりとは解明されていません。しかし、ここまでお読みいただいた皆さんならば、そのあたりさえ十分に解明されれば、これまでの議論を応用して深層学習の場合でもテスト損失の理論保証が可能になるということは理解いただけるかと思います。ここまで理解いただいたならば、ここから先の研究は皆さんにも可能です。ぜひ、考えてみてください。

手前味噌ではありますが、盆地の話など深層ニューラルネットワークの理論については、拙著『深層ニューラルネットワークの高速化』でも深く取り扱っています。また、基本的な話は以下のスライドでも解説しています。ぜひ読んでみてくださいね。

speakerdeck.com

著者情報

この記事がためになった・面白かったと思った方は SNS などで感想いただけると嬉しいです。

新着記事やスライドは @joisino_ (Twitter) にて発信しています。ぜひフォローしてくださいね。

本稿の英語版：A Gentle Introduction to Machine Learning Theory

佐藤 竜馬（さとう りょうま）

京都大学情報学研究科博士課程修了。博士（情報学）。現在、国立情報学研究所助教。著書に『深層ニューラルネットワークの高速化』『グラフニューラルネットワーク』『最適輸送の理論とアルゴリズム』がある。

プロフィールを見る